3.6 Quadratic Inequalities SPM Additional Mathematics

Solve Quadratic Inequalities Intermediate Algebra
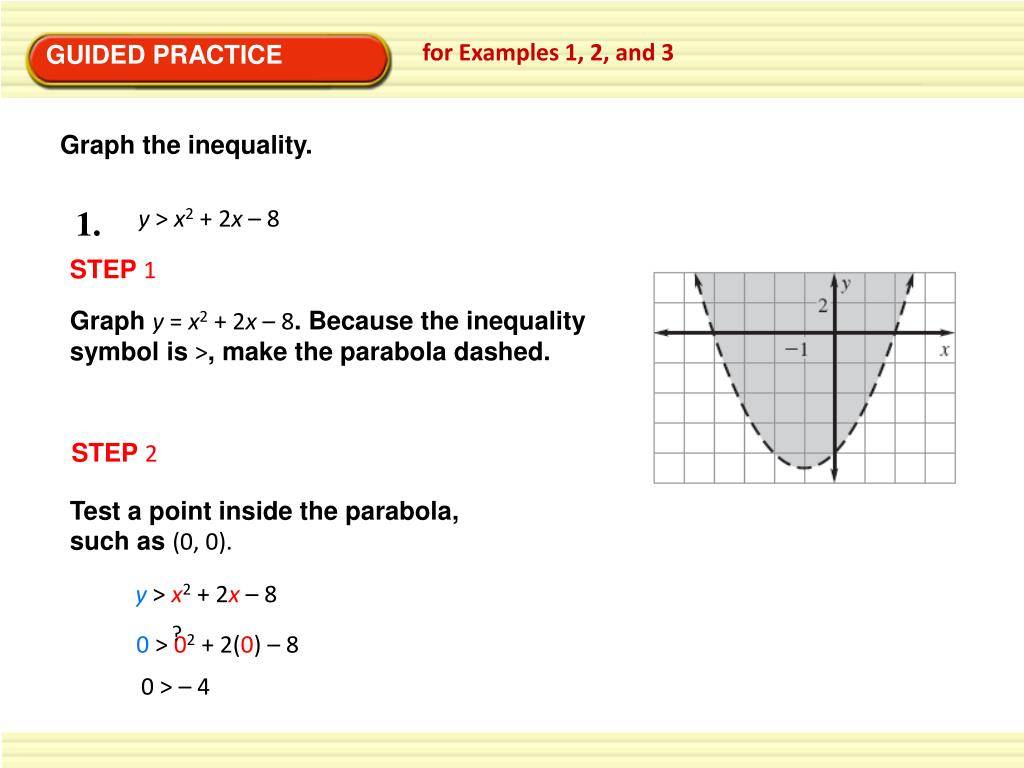
Graphing Quadratic Inequalities. (or substitute <, ≥ <, ≥ or ≤ ≤ for > > ) represents a region of the plane bounded by a parabola . To graph a quadratic inequality, start by graphing the parabola. Then fill in the region either above or below it, depending on the inequality. If the inequality symbol is ≤ ≤ or ≥ ≥ , then the.

Defining quadratic inequalities and graphing their intervals
The second inequality is y is less than 2x minus 5. So if we were to graph 2x minus 5, and something already might jump out at you that these two are parallel to each other. They have the same slope. So 2x minus 5, the y-intercept is negative 5. x is 0, y is negative 1, negative 2, negative 3, negative 4, negative 5.
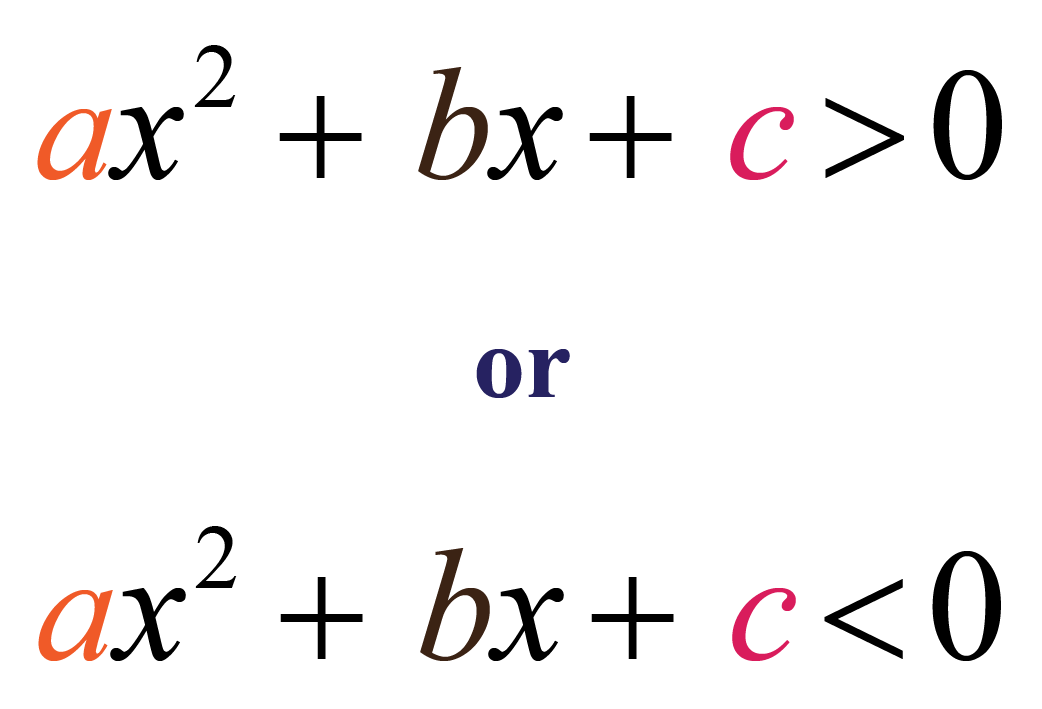
Quadratic Inequalities Graphs Calculator Solved Examples Cuemath
The graph will highlight in green the regions where the graph is above or below zero. Hide/unhide the folders above to switch between the two inequalities. Use the sliders to adjust the values of a, b and c in the quadratic. The red lines will highlight the values of x which correspond to the inequality.

Math Principles Graphs of Quadratic Inequalities
To solve a quadratic inequality ax² + bx + c > d: Draw the line y = d. Determine the points where the parabola ax² + bx + c crosses/touches this line. To find them, solve ax² + bx + (c - d) = 0. If there's no solution, your parabola is entirely above or below the line. Graph the parabola, taking into account the results from Step 2: The arms.

Algebra 1 Worksheets Quadratic Functions Worksheets Quadratics, Quadratic functions
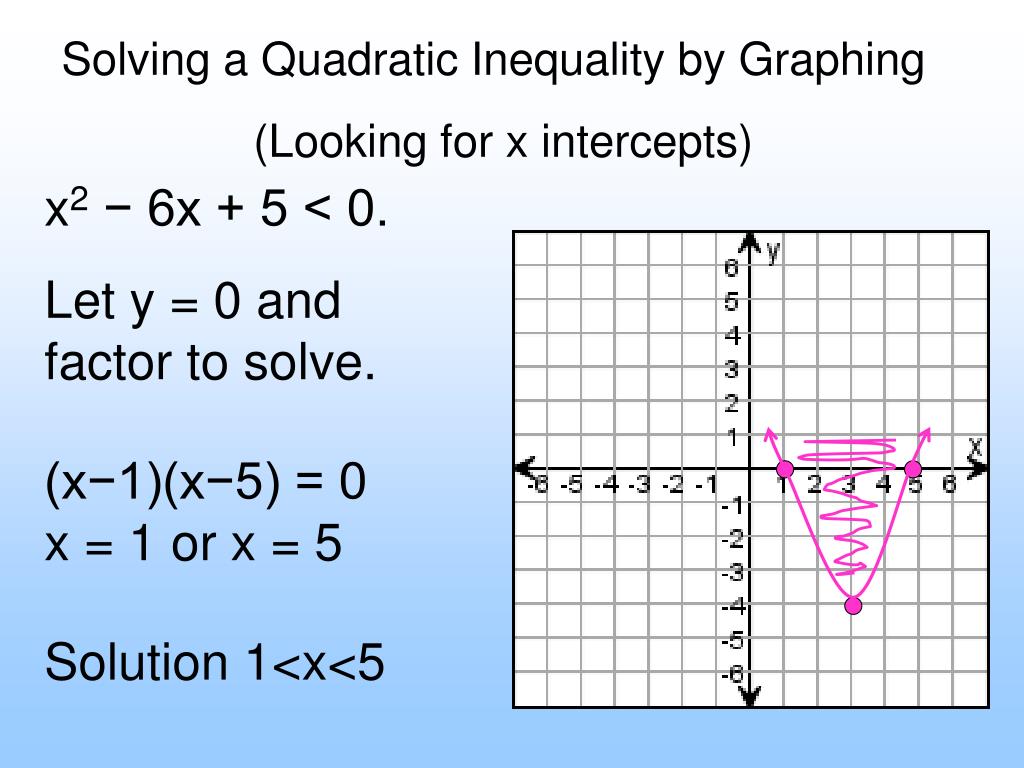
This is a cubic equation (the highest exponent is a cube, i.e. x 3), and is hard to solve, so let us graph it instead: The zero points are approximately: −1.1; 1.3; 2.9; And from the graph we can see the intervals where it is greater than (or equal to) zero: From −1.1 to 1.3, and; From 2.9 on; In interval notation we can write:

3.6 Quadratic Inequalities SPM Additional Mathematics
Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Quadratic Inequalities. Save Copy. Log InorSign Up. x 2 − 5 x − 6. 1. x 2 − 5 x − 6 > 0. 2. x 2 − 5 x.
PPT Graphing Quadratic Inequalities PowerPoint Presentation, free download ID1892142
Video transcript. Welcome to the presentation on quadratic inequalities. Before we get to quadratic inequalities, let's just start graphing some functions and interpret them and then we'll slowly move to the inequalities. Let's say I had f of x is equal to x squared plus x minus 6.

Defining quadratic inequalities and graphing their intervals
Step by step guide to Graphing Quadratic inequalities. A quadratic inequality is in the form \(y>ax^2+bx+c\) (or substitute \(<,≤,\) or \(≥ \) for \(>\)). To graph a quadratic inequality, start by graphing the quadratic parabola. Then fill in the region either inside or outside of it, depending on the inequality. Choose a testing point and.
PPT Graphing & Solving Quadratic Inequalities 5.7 PowerPoint Presentation ID6810018
A quadratic inequality is one that includes an x^{2} term and thus has two roots, or two x-intercepts. This results in a parabola when plotting the inequality on a coordinate plane. Solving an inequality means finding the values of x that.
Solving Quadratic Inequalities YouTube
Write the quadratic inequality in standard form. Graph the function \(f(x)=ax^{2}+bx+c\). Determine the solution from the graph. In the last example, the parabola opened upward and in the next example, it opens downward. In both cases, we are looking for the part of the parabola that is below the \(x\)-axis but note how the position of the.
How to Graph a Quadratic Inequality with 2 Variables Algebra
The Graph of a Quadratic Function. A quadratic function is a polynomial function of degree 2 which can be written in the general form, f(x) = ax2 + bx + c. Here a, b and c represent real numbers where a ≠ 0 .The squaring function f(x) = x2 is a quadratic function whose graph follows. Figure 6.4.1.
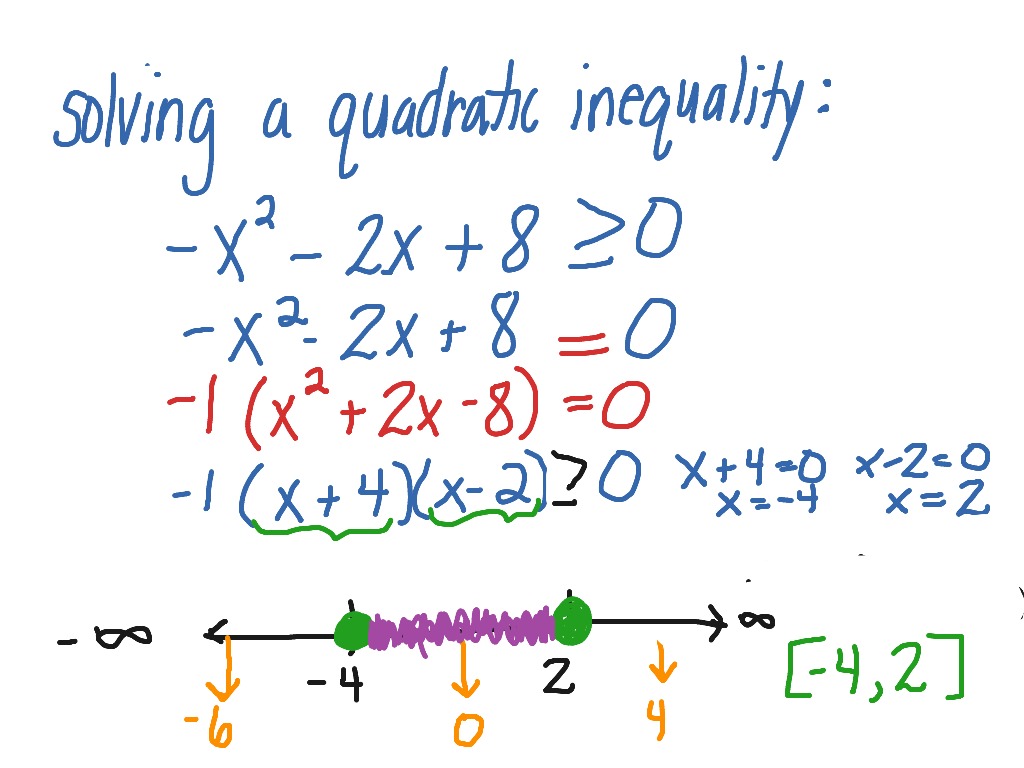
Solving a quadratic inequality (negative in front) Math, Quadratic Inequalities ShowMe
The difference between a quadratic equation and a quadratic inequality is that the quadratic equation is equal to some number while quadratic inequality is either less than or greater than some number. Some examples of quadratic inequalities in one variable are: + x - 1 > 0. + 2x - 1 < 0. The standard form of quadratic inequalities in one.

PPT 4.9 Solving Quadratic Inequalities PowerPoint Presentation, free download ID4887323
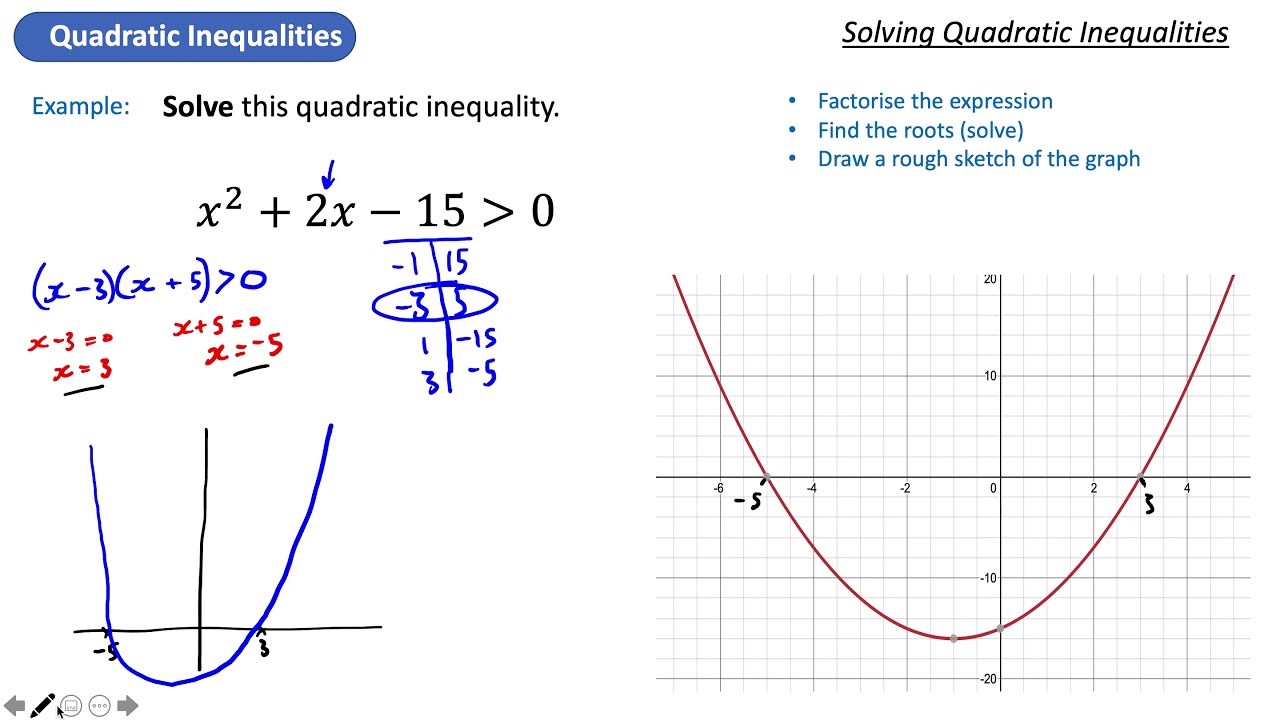
How do you solve quadratic inequalities? To solve a quadratic inequality write the inequality in the standard form ax^2 + bx + c < 0 or ax^2 + bx + c > 0, find the roots of the quadratic equation. Use the roots to divide the number line into intervals. Determine the sign of the expression in that interval.
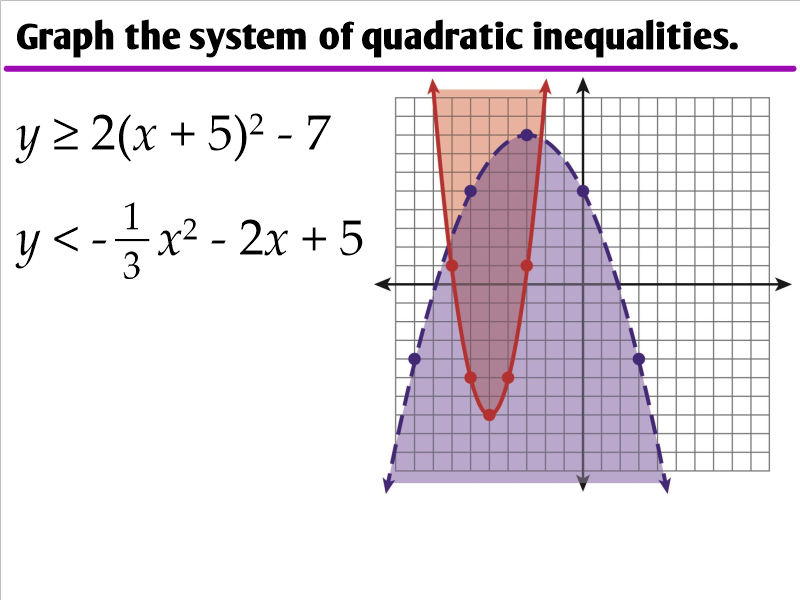
4.6 Graphing Quadratic Inequalities Ms. Zeilstra's Math Classes
You can use the quadratic equation to find the endpoints of the intervals that will be you solution, and would then need to test in which of those intervals the inequality is true. So in this case you could use it to find -5 and 2 [ (-3 +- Sqrt (9+4 (10)1))/2 = (-3 +- 7)/2 = -10/2 or 4/2]. This breaks up the number line into 3 intervals {x<-5.
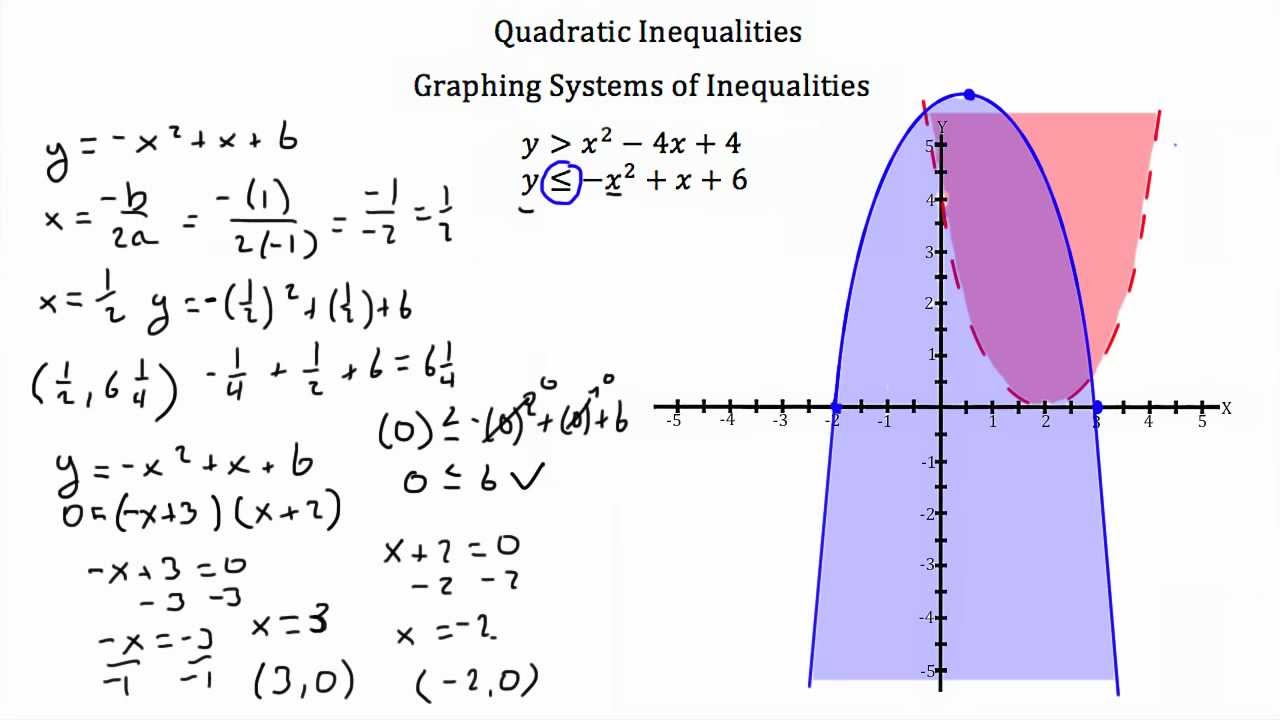
Inequalities with Quadratic Functions YouTube
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright.
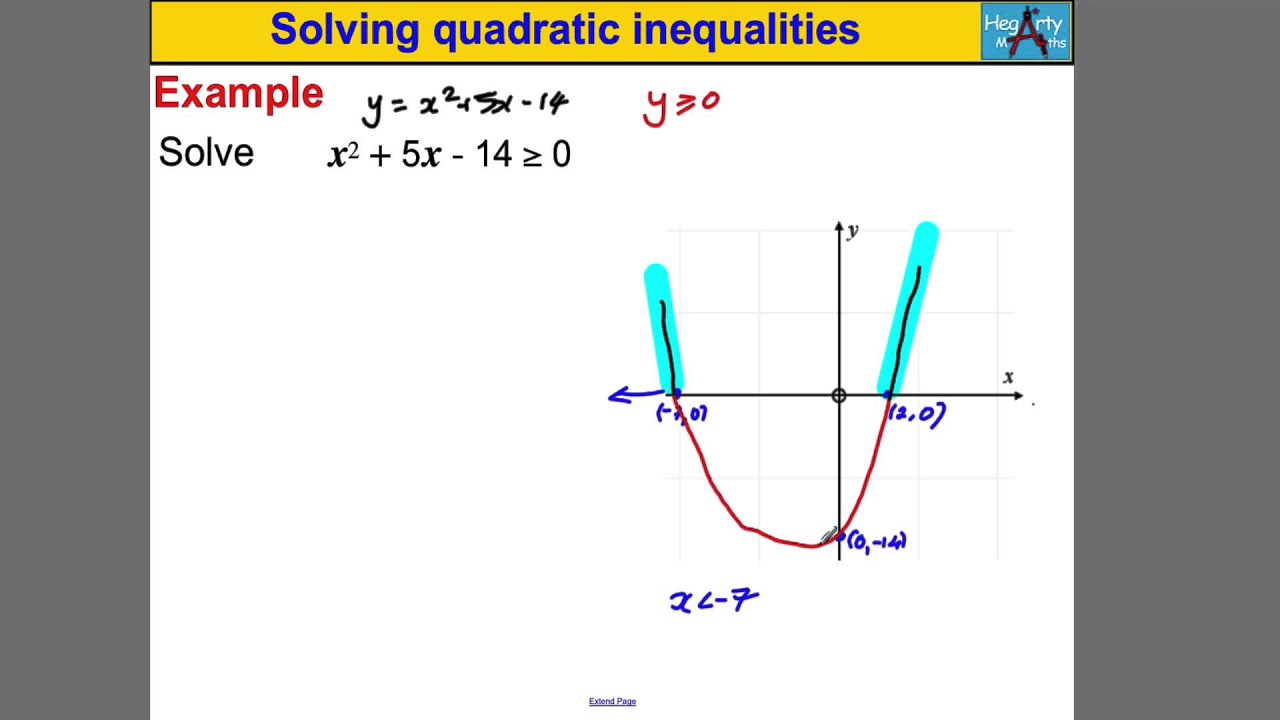
Sketching Graph Quadratic Inequality
It is important to note that this quadratic inequality is in standard form, with zero on one side of the inequality. Step 1: Determine the critical numbers. For a quadratic inequality in standard form, the critical numbers are the roots. Therefore, set the function equal to zero and solve. − x2 + 6x + 7 = 0.